Argiaren abiadurak irakatsitakoa

Argia magikoa da. Denok sentitu izan dugu inoiz hori. Ederra, interesgarria, beharrezkoa… betidanik mirestu izan dugu. Mendeetako lana izan da argiaren izaera eta ezaugarriak ezagutzea, eta oraindik misterio ugari dauden arren, jakintza handia bildu dugu haren inguruan: zer den, nola zabaltzen den, nola jokatzen duen beste elementu batzuekin… Gaurkoan, baina, ez dugu horietan sakonduko, baizik eta nola eraman gintuen gure munduaren ulermena erabat aldatuko zuen teoria ikastera, eta nola lotzen dituen honek argiaren abiadura, denbora eta espazioa.

Argiaren izaera eta propietateak ulertzeko ezagutzen diren lehen teoriak oso aspaldikoak dira. Antzinako Grezian eta Indian erlijio edota jainkoren batekin lotzen zuten normalean, nahiz eta haren ezaugarriak matematikoki ere aztertu zituzten. Beste garai eta pertsona batzuen ekarpena beharrezkoa izan bazen ere (ikus Ibn al-Haytham), aurrerapen esanguratsuenak XVII. mendean iritsi ziren, Ilustrazioaren garaian [1]. Kepler, Descartes, Newton, Hooke, Young eta beste hainbat zientzialarik modelo ezberdinak proposatu zituzten: partikula edo uhin izaera, hedatze-bide ezberdinak, abiadura aldaketak… baina pausu garrantzitsuena XIX. mende erdialdean iritsi zen, Michael Faradayk argia elektromagnetismoarekin lotuta zegoela erakutsi zuenean; are eta gehiago, eremu elektromagnetikoaren bibrazioa zela proposatu zuen [2]. Garai hartan gero eta gehiago zekiten elektromagnetismoaren inguruan, esperimentu asko egin baitziren karga elektriko, iman eta haien elkarrekintzarekin, baina emaitza guzti horiek modu bateratuan azalduko zituen modeloa falta zen. Hemen iritsi zen gure gaurko lehenengo protagonista: James Clerk Maxwell.

Maxwellen ekuazioak

Maxwell fisikari eskoziarrak eremu elektromagnetikoaren jokaera eta elkarrekintzak erabat azaltzen zituen teoria sortu zuen, fisikaren historiako lorpen handienetako bat erdietsita. Argia, karga elektrikoak eta haien mugimendua, indar elektriko eta magnetikoak… dena bateratu zuen marko teoriko dotore batean. Bere formulazioa ezberdina izan bazen ere, egun “Maxwellen ekuazio” moduan ezagutzen ditugun lau ekuaziotan laburtu daiteke modelo hori:

1. irudia: Maxwellen ekuazioak, non E eremu elektrikoa den, B eremu magnetikoa, 𝜌 karga elektriko dentsitatea, j korronte dentsitatea eta 𝜀₀ eta  𝜇₀ hutsaren permitibitatea eta iragazkortasuna, hurrenez hurren. Ekuazio horiek eremu elektromagnetikoaren izaera eta propietateak deskribatzen dituzte.

Maxwellen ekuazioek E eremu elektrikoaren eta B eremu magnetikoaren propietateak definitzen dituzte, eta haien arteko elkarrekintza deskribatu. Ekuazio horietan bi konstante agertzen dira: 𝜀₀ permitibitatea eta 𝜇₀ iragazkortasuna, hau da, zeinen “erraza” ala “zaila” den hutsean eremu elektriko eta magnetikoak sortzea, hurrenez hurren. Teoria horrek arrakasta handia izan zuen, eremu elektriko eta magnetikoaren jokaera oso ondo deskribatzen zituelako, baina beste emaitza garrantzitsu bat ere azaleratu zuen. Kontua da, Maxwellen ekuazioekin apur bat jokatuta, eremu elektromagnetikoak uhinak sortzen dituela ondoriozta daitekeela, eta uhin horien abiadura (konstantea) c = 1/𝜀₀𝜇₀  (300.000 km/s gutxi gorabehera) aldez aurretik neurtutako argiaren abiadura dela! Hala, Maxwellek argia erradiazio elektromagnetikoa zela baieztatu ahal izan zuen.

“Ba oso ondo” pentsatuko du irakurleak, “eta zer zerikusi du horrek denbora eta espazioarekin?”. Bada, Maxwellen ekuazio eder horiek fisikaren printzipio garrantzitsuenetako bat urratzen zuten: Galileoren erlatibitatea.

Galileoren erlatibitate printzipioa

Galileo Galilei zientzialari ezagunak XVII. mendean proposatutakoa azaltzeko, lehenengo erreferentzia-sistema inertzialak ulertu behar ditugu. Erreferentzia-sistema horietan inertziaren printzipioa betetzen da: kanpoko indarren eraginik jasaten ez duen gorputzak abiadura konstantea dauka. Adibide bat jartzearren, jo dezagun autobus batean bidaiatzen ari garela. Berehala nabarituko dugu autobusa azeleratzen ala frenatzen ari den, baina kristalak tapatuko bagenitu, ez genuke autobusa geldi ala abiadura konstantean (teknikoki higidura zuzen uniformea) doan bereizteko modurik izango (autobusak soinurik egiten ez duen eta errepideak perfektuak diren egoera idealaz ari gara). Azken bi egoera horiek erreferentzia-sistema inertzialak dira; lurrean geldi uzten dugun pilota geldi geratuko da, ez du ez aurrera eta ez atzera egingo.

Erreferentzia-sistema horiek ulertuta, Galileoren printzipioa honakoa da: fisikaren legeak berberak dira erreferentzia-sistema inertzial guztietan. Horrek esan nahi duena da esperimentu guztiek emaitza bera emango dutela geldi dagoen eta higidura zuzen uniformean mugitzen ari den autobusean; autobus barruan egonda ez dago bi egoera horiek bereizteko modurik! Ondorioz, geltokian dagoen A autobus barruko behatzaileak esan dezake bera geldi dagoela eta aurretik pasatzen ari den B autobusa mugimenduan dagoela, baina B autobuseko behatzaileak esan dezake bera dela geldi dagoena, eta A autobusa doala atzera martxan. Fisikaren ikuspuntutik, batak ez du besteak baino arrazoi gehiago, biek baitute geldi daudela esateko eskubide bera! Zentzu horretan, ez dago jakiterik geldi gauden ala mugitzen ari garen.

Testuinguru horretan, Galileok elkarrekiko v abiadura konstantean mugitzen ari diren bi erreferentzia-sistema inertzialen arteko transformazioak eman zituen. S erreferentzia-sisteman edozein gertakariren koordenatuak (t, x, y, z) dira (noiz gertatu den eta hiru dimentsioko espazioaren zein puntutan) eta S’ erreferentzia-sisteman, aldiz, (t’, x’, y’, z’). Hori horrela, hauek dira koordenatu horien arteko transformazioak (t = t’ = 0 unean S eta S’ puntu berean zeudela asumituta):

2. irudia: Galileoren transformazioak. Ekuazio horiek bi erreferentzia-sistema inertzialen arteko denbora eta espazio koordenatuen bihurketa adierazten dute. Guretzat intuitiboak diren aldaketak deskribatzen dituzte eta mekanika klasikoaren oinarria osatzen dute.

Transformazio horiek ulertzea erraza da: geltokian dagoen A autobusetik gertakari bat t = 1 s eta x = 10 m koordenatutan gertatu dela ikusten badugu, x norabidean v = 1 m/s abiaduran doan B autobuseko behatzaileak t’ = 1 s eta x’ = 9 m koordenatutan gertatu dela ikusiko du, segundo horretan metro bat aurreratu baitu. y eta z koordenatuak, aldiz, ez dira aldatuko.

Galileoren transformazioek guretzat intuitiboa den errealitatea deskribatzen dute. Hori ulertzeko, jo dezagun kotxe baten abiadura neurtu nahi dugula. Gu, S erreferentzia-sistema, errepidearen bazterrean gaude, eta gure laguna, S’, trenean doa kotxearen norabide berean v = 30 km/h abiaduran. Gure ikuspuntutik gu geldi gaude (jakina!) eta kotxea 90 km/h abiaduran doala neurtzen dugu; zer neurtuko du gure lagunak? Modu formalagoan adierazita, S erreferentzia-sisteman neurtzen dugun kotxearen abiadurari u deitzen badiogu, zein izango da S’ erreferentzia-sisteman neurtzen den kotxearen u’ abiadura? Abiaduraren definizioa erabilita (distantziaren deribatua denborarekiko) eta t’ eta x’ Galileoren transformazioekin ordezkatuta ondorengo formula lortzen dugu:

Hau da, gure lagunak esango du bera dela geldi dagoena, eta kotxea u' = u - v = 90 km/h - 30 km/h = 60 km/h abiaduran doala neurtuko du (eta gu -30km/h abiaduran goazela). Posizioak eta abiadurak gehitzeko modu hori deskribatzen dute Galileoren transformazioek,  eta “geldi” eta “mugitzen” kontzeptuak erlatiboak direla azpimarratzen dute, ez dagoela horiek definitzeko modu absoluturik.

Galileoren erlatibitatea ondo ulertutako eta onartutako printzipioa zen XIX. mendean, baina argiak abiadura bat izateak arriskuan jarri zuen dena. Maxwellen ekuazioak ikusita, argiaren abiadura neurtzean c = 1/𝜀0𝜇0  neurtzen zuenak geldi zegoela esan ahalko zuen, eta gehiago edo gutxiago neurtzen zuenak argiaren norabidearen kontra edo alde mugitzen ari zela, hurrenez hurren. Posible al da unibertsoak geldi gauden ala ez jakiteko aukera ematea?

Nola konpondu arazoa?

Maxwellen ekuazioak garatu ondorengo hamarkadetan fisikari asko ibili ziren zalantza horiek argitu nahian. Posible zen argiak abiadura bakarra izatea? Neurtu zitekeen zer/zein dagoen unibertsoan “benetan geldi”? Galdera horiek argitzeko lehenengo pausua “eter argitsua” bilatzea izan zen. Soinu-uhinek hedatzeko airea behar duten moduan, edo itsasoko olatuek ura, fisikari askoren ustez egon behar zuen argiak hedatzeko erabiltzen duen material ikusezin bat, eter izena jasotzen zuena. Hala bazen, posible izango litzateke material horrekiko abiadura neurtu eta benetan geldi dagoen erreferentzia-sistema identifikatzea, Galileoren erlatibitatea baztertuta. Hortaz, XIX. mende amaieran hori neurtzeko esperimentuak egin ziren (Michaelson-Morley esperimentua da ezagunena), eta ondorio harrigarri batera iritsi ziren: berdin du zein momentutan edo zein norabidetan neurtu argia, lurraren edozein mugimendurekiko, argiaren abiadura beti berdina da, c [3]. Halako esperimentuek eterra existitzen ez zela iradoki zuten, eta argiaren abiadura beti dela konstantea, edozein abiaduran eta norabidetan mugitzen den behatzaile ororentzat. Lehen jarritako adibidea jarraituta, argiaren abiadura berdin-berdina neurtuko genuke errepide bazterretik zein trenetik. Baina hori nola da posible? Hori ez da Galileoren transformazioek esaten digutena!

Egun ezagutzen dugun teoriara iristeko fisikari eta matematikari askoren lana behar izan zen: FitzGerald, Lorentz, Poincaré… baina azken pausua 1905. urtean eman zen. Hemen dator gure gaurko bigarren protagonista: Albert Einstein. Mugimenduan dauden sistema elektromagnetikoen kontextuan, gerora erlatibitate berezia izenarekin ezagutzen den teoria aurkeztu zuen [4].

Erlatibitate berezia

Erlatibitate berezia espazioa eta denboraren arteko harremana deskribatzen duen teoria da. Hori garatzeko, Einsteinek bi postulatu hartu zituen oinarri:

1. Erlatibitatearen printzipioa: lege fisikoak berdinak dira erreferentzia-sistema inertzial guztietan. Fisika berdina da higidura zuzen uniformean ala geldirik dagoen behatzaile ororentzat.

2. Argiaren abiaduraren aldaezintasunaren printzipioa: argiaren abiadura ez da behatzailearen araberakoa, beti neurtuko da c = 300.000 km/s.

   
   

Hortaz, Einsteinek bateraezinak diruditen bi printzipioak hartu zituen oinarritzat, bigarrenak ez baititu lehenengoarekin lotutako transformazio arauak inola ere betetzen. Nola bateratu zituen teoria batean? Nola funtzionatzen du erlatibitate bereziak?

Bada, aipatutako bi printzipioak bateragarriak dira erreferentzia-sistema ezberdinen espazio eta denbora koordenatuen arteko transformazio berriak definitzen badira: Lorentz-en transformazioak (Hendrik Lorentz fisikariaren omenez).

3. irudia: Lorentzen transformazioak. Bi erreferentzia-sistema inertzialen arteko denbora eta espazio koordenatuen bihurketa deskribatzen dute. Ekuazio horiek denbora eta espazioa absolutuak ez direla adierazten dute, eta unibertsoa eta bere propietateak ulertzeko modua erabat aldatu zuten.

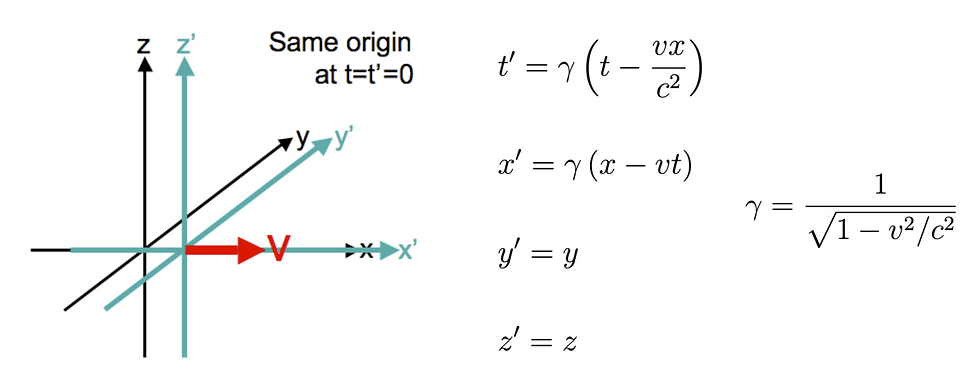
Erreferentzia-sistemen arteko transformazio berri hauek ez dira batere intuitiboak eta erabateko paradigma aldaketa susposatu zuten fisikan. Galileoren transformazioan oinarritzen den mekanika klasikoan denbora absolutua da, behatzaile guztientzat berdina. Halaber, espazioa ere konstantea da, ez da erreferentzia-sistemaren arabera luzatu edo uzkurtzen. Modelo horretan unibertsoa eszenatoki finko bat da, non dena erloju unibertsal baten arabera gertatzen den. Lorentzen transformazioetan oinarritzen den erlatibitate berezian, ordea, denbora ez da absolutua, ezta espazioa ere. Bata zein bestea behatzailearen higiduraren araberakoak dira, eta ezberdin neurtuko dira erreferentzia-sistema ezberdinetan. Hortaz, bi elementu horiek ez daude bananduta; espazio-denbora izeneko lau dimentsioko ingurunea osatzen dute, eta ingurune horretan espazioa eta denbora ezberdin neurtuko dira mugimenduaren arabera. Hala ere, aipatzekoa da Galileoren transformazioak ez direla erabat okerrak; erreferentzia-sistemen arteko abiadura erlatiboa argiaren abiadura baina askoz txikiagoa denean (v ≪ c) lortzen diren emaitzen hurbilketa dira.

Lorentzen transformazio eta erlatibitate bereziaren ondorioak hobeto ulertzeko, lehen jarritako adibidea hartuko dugu berriro. Oraingoan, baina, erlatibitatearen efektuak argiago ikusteko, ibilgailu bereziak beharko ditugu, benetan azkar higitzen direnak. Kotxeak 90 km/h ordez argiaren abiaduraren %90 izango du, hau da, 0.9c, eta trenak, aldiz, 30 km/h beharrean argiaren abiaduraren %30, 0.3c, S erreferentzia-sisteman (gure sisteman) neurtuta. Aldi berean, kotxe eta trenaren norabidean argi izpi bat bidaliko dugu. Zer neurtuko du gure lagunak trenetik? Zein abiaduran doaz kotxea eta argia?

Erlatibitate bereziak dioenaren arabera, abiadurak ez dira besterik gabe gehitzen Galileoren transformazioekin gertatzen zen moduan. Lehen egindako prozesu bera gauzatzen badugu, baina oraingoan Lorentzen transformazoekin, honakoa lortuko dugu:

Hau da, gure lagunak, bere S’ erreferentzia-sistematik kotxea u' = (u - v)/(1 - uv/c²) = (0.9c - 0.3c)/(1 - 0.9*0.3) = 0.82c abiaduran doala neurtuko du (gogoratu Galileoren transformazioen arabera 0.9c - 0.3c = 0.6c neurtuko genukeela!). Guk c abiaduran neurtzen dugun argi izpia, aldiz, u' = (u - v)/(1 - uv/c²) = (c - 0.3c)/(1 - 1*0.3) = c abiaduran doala neurtuko du, guk bezalaxe. Izan ere, idatzitako formulan argi ikus daiteke gure sistematik neurtzen dugun abiadura u = c bada beste edozein S’ sistematik ere neurtzen dugun abiadura u' = (c - v)/(1 - cv/c²) = c (1 - v/c)/(1 - v/c) = c izango dela; argia c abiaduran doa edozein sistemako edozein behatzailerentzat, nahiz eta argiaren norabidearen alde ala kontra higitu. Nahiz eta orain ez dugun honetan sakonduko, emaitza horiek gauza interesgarri bat ikusarazten dute: c ez da “argiaren abiadura” soilik, bizi garen espazio-denboraren berezko propietate bat baizik. Ez da kasualitatea konstante hori Lorentzen transformazioetan, Einsteinen E = mc² formula ezagunean eta beste mila tokitan agertzea!

Ondorioak

Modu horretan Albert Einsteinek (beste fisikari eta matematikari askoren lanean oinarrituta) bateraezinak ziruditen bi printzipio lotu zituen. Alde batetik, Galileoren erlatibitate printzipioa errespetatu zuen: inork ezin du esan modu absolutuan bera dagoela geldi eta gainontzekoak mugitzen, unibertsoak ez baitu hori bereizteko modurik ematen. Denok gaude geldi gure erreferentzia-sisteman hala erabakitzen badugu! Beste alde batetik, argiak behatzaile guztientzako c abiadura duela erakutsi zuen, eta horrek ez duela zertan erlatibitate printzipioa urratzen. Hori bai, horretarako espazioa eta denboraz genekien guztia aldatu behar izan zuen!

Erlatibitate bereziak baditu beste mila inplikazio: nola pasatzen den astiroago denbora behatzaile batzuentzat, nola uzkurtzen diren neurtutako distantziak neurtzen dituenaren abiaduraren arabera, nola mugatzen duen c abiadurak unibertsoan edozerk har dezaken abiadura, nola behatzaile batentzat une berean gertatzen diren bi gertakari beste behatzaile batentzat une ezberdinetan gertatzen diren… baina zer edo zer utzi beharko da beste artikulu batzuetan argitzeko!

Erreferentziak

[1] J. J. O'Connor and E. F. Robertson, "The History of Light," MacTutor History of Mathematics Archive, University of St Andrews. [Online]. Available: https://web.archive.org/web/20170319180859/http://www-groups.dcs.st-and.ac.uk/history/HistTopics/Light_1.html

[2] Wikipedia contributors, "Understanding Physics (Cassidy). [Online]. Available: https://es.wikipedia.org/wiki/Understanding_Physics_(Cassidy)

[3] A. A. Michelson and E. W. Morley, "On the Relative Motion of the Earth and the Luminiferous Ether," American Journal of Science, vol. 34, no. 203, pp. 333–345, Nov. 1887.

[4] A. Einstein, "Zur Elektrodynamik bewegter Körper," Annalen der Physik, vol. 17, no. 10, pp. 891–921, 1905.