Urrezko zenbakia: harmonia matematikoa naturan

Irene
3 ago
6 Min. de lectura

Actualizado: 4 ago

Zein da edertasunaren formula? Harmoniaz betetako paisaia bat, arte lan baten oreka perfektua, gorputzaren proportzio orekatua… Hauek guztiek lilura sortzen digute. Baina zer iruditzen esango bagenu edertasun hori guztia zenbaki bakar batekin azal daitekeela?

Zenbaki horri urrezko zenbakia deitzen zaio. Matematika eta natura era zuzenean uztartzen dituen konstante misteriotsu honek historian zehar hainbat zientzialari, filosofo eta artista txunditu ditu.

Sarritan pentsatzen dugu matematika tresna abstraktu eta hotza dela, eguneroko bizitzatik urrun dagoena. Baina urrezko zenbakia kontrakoa frogatzeko adibide paregabea da, izan ere, teoria hutsetik haratago, munduaren egitura azaltzen laguntzen du. Artikulu honetan, matematikako definizio soiletik hasita, bere presentzia aztertuko dugu naturan, gorputzean, artean eta egunerokoan. Prest al zaude matematikaren edertasuna ezagutzeko?

Definizioa

Urrezko zenbakia, φ (phi) hizki grekoarekin idazten dena, zenbaki irrazional¹ bat da eta bere balioa 1,618… da gutxi gorabehera. Zenbaki hau definitzeko hainbat modu daude.

Definizio formalarekin hasiko gara. Zuzen baten a eta b bi segmentuk elkarren artean gordetzen duten proportzioaren zenbakizko balioa da, a segmentua b baino luzeagoa izanik eta honako erlazioa betetzen dutelarik:

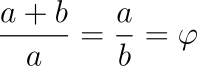
φ-ren balio zehatza kalkulatzeko, ekuazioa sinplifikatu, a/b = φ dela kontuan hartuz:

Bigarren mailako ekuazioaren soluzio positiboa hartzen bada, aipatu dugun balioa lortzen da, hau da,

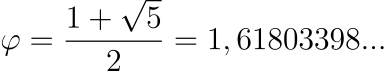
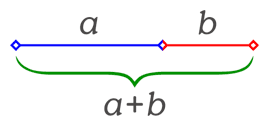
1. irudia: Zenbakia segmentuen zatiketen bidez lortzen da, proportzio hau kontuan hartuz: a+b luzera osoa zati a eta a zati b berdinak dira.

Zenbaki hau lortzeko beste modu bat luzera unitariodun AB eta BC bi segmentu perpendikular hartzea da. Ondoren, B eta C puntuen erdiko O zentrotik ½ erradioko zirkunferentzia marrazten da, gero A eta O puntuak lotzeko. Horrela, 2. irudian ikusten den P puntua lortuko dugu. Urrezko zenbakia AP segmentuaren luzera izango da.

2. irudia: A puntutik P puntura dagoen distantzia φ da.

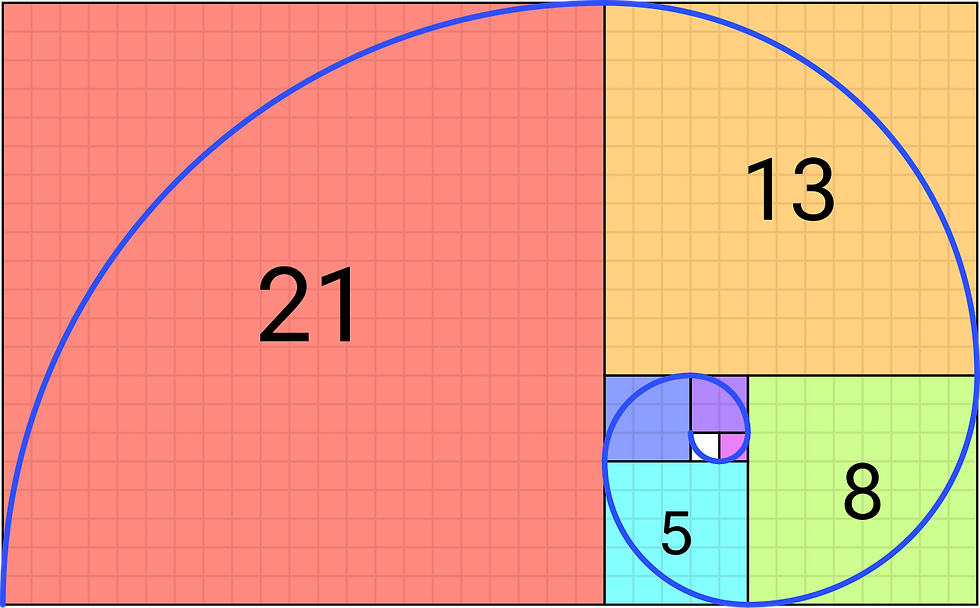
Urrezko zenbakiak Fibonacciren segidarekin lotura estua du. Segida hau 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,... da, hau da, zenbaki bakoitza aurreko bi zenbakien arteko batura. Matematikoki idatziz, Fibonacciren segida

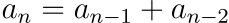
da, a0 = 0 eta a1 = 1 izanik. Baina, zer zerikusi du segida honek urrezko zenbakiarekin? Bada, zenbaki baten eta aurreko zenbakiaren arteko zatidura,

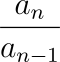
, geroz eta gehiago hurbiltzen dela φ baliora. Hau da,

Esate baterako, 21/13=1,615… edo 34/21=1,619… urrezko zenbakiaren hurbilpenak dira.

3. irudia: Fibonacciren espirala. Urrezko espiralaren hurbilpen bat da, segidako zenbakien tamainako karratuen izkinetatik arku zirkularrak marraztuz lortzen dena.

Beste adierazpen matematiko batzuk

Urrezko zenbakia ez da edonolako zenbaki irrazionala, izan ere, aipatu bezala bizitzan presentzia asko du. Hala ere, bere egitura matematikoa bereziki interesgarria da, hainbat adierazpen bitxi dituelako, bere harmonia modu matematikoan ere adierazten duena.

Alde batetik, adierazpen berezi bat zatiki jarraituen bidezkoa da, lortu dugun

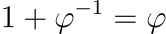
ekuazioa behin eta berriz ordezkatuz,

Honako hau φ zenbakiaren jarraipen infinitua da eta ikusten den bezala oso simetriko eta errepikakorra da. Gainera, zatiki jarraitu guztietatik sinpleena da eta konbergentzia mantsoena duena. Propietate hori dela eta, zenbaki arrazional batekin hurbiltzea oso zaila da. Bereziki, zenbaki arrazionaletatik urrunen dagoen zenbakia da eta horregatik, zenbaki “irrazionalena” dela esaten da.

Bestalde, erro karratu infinituen bitartez ere idatz daiteke. Horretarako,

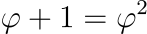
ekuaziotik abiatuz,

lortuko dugu. Berriro ere, adierazpen hau behin eta berriz ordezkatuz, urrezko zenbakiaren beste propietate autoerrepikakorra lortzen da.

Forma matematiko hauek bere buruarekiko duen mendekotasun sinplea erakusten dute. Horrek urrezko zenbakiari harmonia eta simetria ematen dio, bai matematikoki, baita bisualki ere. Gainera, adierazpen horien bidez ulertzen da zergatik deitzen zaion zenbaki perfektu estetiko.

Historia

Urrezko zenbakiaren kontzeptua ez da modernoa, izan ere, Antzinako Grezian aztertu zen lehen aldiz Pitagorikoen eskutik. Ondoren, Euklidesek jada idatzita utzi zuen proportzio hau “banaketa harmoniko” bezala. Gainera, Euklidesek φ zenbaki gisa adierazi ez zuen arren, haren definizio formala eta kalkuluak eman zituen lehen aldiz.

Erdi Aroan, arabiar matematikariek eta geroago italiarrek egitura hori ikertzen jarraitu zuten. Adibidez, Fibonaccik argitaratutako “Liber Abaci” (1202) lanean agertzen den bere segida famatua ez zen urrezko zenbakiarekin erlazionatu hasiera batean, baina geroago argi geratu zen haien arteko harremana. Lan horren ostean, segida horrek Europa osoko zientzialari askoren interesa piztu zuen.

XVI. mendean Luca Paciolik proportzio horri “divina proportione” izena jarri zion, idatzi zuen liburuari bezalaxe. Lan horrek artearen munduan eragin handia izan zuen, Leonardo da Vincik liburua ilustratu zuelarik. Biak ados zeuden: ez zen soilik edertasunaren oinarria, unibertsoaren ordenaren oinarria baizik. XIX. mendean “urrezko proportzioa” izena hartu zuen eta hurrengo urteetan bere mitifikazioa areagotu zen, batez ere arte eta diseinuaren munduan. Gaur egun, zientzialariek sistema desberdinetan agertzen dela frogatzen saiatzen ari dira oraindik.

Loturak

Aipatutako guztia garrantzitsua da noski, urrezko zenbakia zer den ulertzeko eta bere garapenaren jarraipena egiteko, baina benetako gakoa orain dator: unibertsoarekin duen lotura. Izan ere, teoria matematiko bat izateaz gain, φ-ren benetako lilura haren aplikazioetan datza.

Naturan:

Urrezko zenbakiaren agerpena naturan txundigarria da. Fenomeno askok erakusten dute egitura biologiko ugarik antzekotasunak dituztela patroi matematikoekin.

4. irudia: eguzki-loreen espiral kopurua beti zaingo da Fibonacciren segidako zenbakiren bati. Irudiko loreen kasuan 21 eta 34.

Esate baterako, eguzki-loreen haziak haien zentrotik kanporantz antolatuta daude, espiral formarekin. Gainera, espiral kopuruak Fibonacciren segidaren zenbakiak izaten dira eta proportzio horien zatidurak φ zenbakiaren hurbilketak. Itsas maskorrekin ere antzekoa gertatzen da, izan ere, nautilus maskorrek lehen aipatutako urrezko espiralaren itxura edukitzen dute. Kontuan hartu behar da fenomeno hau ez dela guztiz zehatza, baina antzeko eredua dela. Bestalde, erlauntzetan dauden erleen eme eta arren arteko populazio proportzioa Fibonacciren segidarekin erlazionatuta dago, erleen ugalketa prozesuagatik. Horregatik, eme kopurua ar kopuruarekin zatitzen bada edozein erlauntzetan, φ-ren hurbilpen bat lortuko dugu. Beste hainbat adibide daude natura eta urrezko zenbakia lotzen dituztenak, hala nola, zuhaitzen adarren banaketa, pinaburuen espiralak edota landareen filotaxia.

5. irudia: itsas maskorren espiralek urrezko espiralaren forma izaten dute, Fibonaccirenak bezala.

Gorputzean:

Gizakion gorputzak ere oso harreman estua du urrezko zenbakiarekin, nahiz eta hori frogatzea beti ez den erraza. Le Corbusier arkitektoak “Modulor” izeneko sistema bat sortu zuen XX. mendearen erdialdean, diseinu arkitektonikorako eskala harmonikoa definitzeko. Harrigarriena da sistema hau sortzen ari zen bitartean, giza gorputzaren neurriak φ-rekin zuten erlazio zuzenaz ohartu zela.

Adibidez, zure altuera osoa lurretik zilborrerako distantziarekin zatituz, 1,618 zenbakira hurbilduko da. Bestalde, sorbaldatik hatz puntetarainoko distantzia zatitu ukondotik hatz puntetarainoko distantziarekin eta hemen ere 1,618 lortzen da. Gauza berdina gertatzen da aldakatik lurrerako eta belaunetik lurrerako distantziarekin edota esku eta oinetako artikulazioekin.

Hori guztiagatik, gorputzaren neurriek urrezko proportzioa jarraitzen dutela esaten da, baina lotura hau ez da beti zehatza. Hala ere, sistema honek erakusten du gizakiak harmonia bilatu nahi izan duela baita bere irudian ere.

Artean:

Artearen historian ere nahiko presente daukagu, bereziki margolaritzan, musikagintzan eta arkitekturan, harmonia lortzeko. Askotan aipatzen da Antzinako Greziako Partenoia urrezko zenbakiaren adibide gisa, bere fatxadaren altuera eta zabaleraren arteko proportzioagatik edota bere zutabeen egituragatik.

Leonardo da Vinci artistak ere harreman estua du urrezko zenbakiarekin. Hasteko, aipatu bezala Paciolik argitaratutako “De Divina Proportione” lanaren irudiak marraztu zituen, hala nola zenbait poliedro konplexu. Horiek da Vinciren interes eta ezagutza sakona erakusten dute φ-ren inguruan. Gainera, bere koadroetan ere ikus daitezke proportzio harmonikoaren erabilerak. Adibide argia da marraztu zuen “Vitruvius gizakia”, lehen aipatu ditugun neurri idealak jasotzen dituena.

6. irudia: Leonardo da Vincik marraztutako Vitruvius gizakia, proportzio harmonikoekin.

Musikagintzan ere urrezko proportzioaren agerpenak daudela esaten da, abesti baten klimaxaren kokapenean adibidez. Nahiz eta ez dagoen frogarik Bach, Mozart eta Beethoven konpositoreek φ kontzienteki erabili zutenik, haien musikan maiz agertzen da. XX. mendean aldiz, nabarmenagoa izan da urrezko zenbakiaren erabilpena musikan, Béla Bartóren eskutik besteak beste.

Egunerokoan:

Nahiz eta ez ohartu, eguneroko bizitzan ere urrezko zenbakia leku askotan topa dezakegu, hala nola, diseinu grafikotan edo objektu industrialen neurrietan. Web orrialde askotan kontuan hartzen da irudien kokapenerako, edukiaren marjinarako edo nabigazio barrarako. Arkitekturan ere kontuan hartzen da ateen eta leihoen tamainarako edo altzairuen diseinurako. Bestalde, argazkigintzan edo produktuen diseinuan ere askotan erabiltzen dira urrezko laukia eta espirala. Azkenik, enpresa askoren logotipoak proportzio harmonikoan diseinatu dira, adibidez, Twitter, Pepsi edo Apple. Hala ere, kontuan izan behar da kasu askotan urrezko zenbakia ez dela zehaztasun matematikoz aplikatzen. Hau da, askotan intuizio estetikoak gidatutako erabakiak izaten dira, baina aztertuz gero, φ-ren antzeko proportzioak ikus daitezke.

Zalantzak eta mitoak

Aurretik aipatutako adibide guztiak nahiko txundigarriak diren arren, ikuspegi kritiko batetik landu behar dira. Izan ere, ikusi dugun bezala oso erraza da urrezko zenbakiarekin erlazionatutako adibideak topatzea, eta hori ez da beti zorroztasun osoz aztertzen. Kasu askotan, antzekotasun bisualak eta zenbakizko hurbilketak egiten dira proportzio hau ikusteko, nahiz eta egiazki nahigabe erabili den. Nautilus maskorraren kasua adibide garbia da, neurketek erakusten baitute forma espiral logaritmiko orokor bat dutela, baina kasu askotan ez dela zehazki urrezko espirala.

Hori dela eta, ikuspegi zorrotz bat mantentzea komeni da: φ zenbaki interesgarria da, baina ez da unibertsoaren giltza. Bere presentzia fenomeno askotan nabaria den arren, beste hainbat kasutan gure interpretazio estetikoak soilik izaten dira.

Ondorioak

Urrezko zenbakia, φ, zenbaki arrunt bat baino gehiago da: matematika eta bizitzaren arteko zubia. Bere definizio matematikoa nahiko sinplea den arren, horren atzean unibertsoaren antolaketaren harmonia ezkutatzen da. Zaila da horrenbeste diziplinatan agertzen den beste konstante bat aurkitzea. Eguzki-loreen hazietatik musikagintzaraino, Partenoiko egituratik Leonardo da Vinciren marrazkietaraino edota Pepsiren logotipotik gorputzaren neurrietaraino. Urrezko zenbakiak presentzia iraunkor bat du, modu ikusgai edo ezkutuan, gure inguruan.

Hala eta gutiz ere, proportzio honen lilurak arriskua ere badakar: gehiegizko idealizazioa. Ez da ahaztu behar batzuetan φ-ren presentzia interpretazio estetikoaren ondorioa dela, eta beti ez dela ikuspegi zientifikotik aztertzen.

Azken finean, urrezko zenbakia ez da magikoa, baina bai harrigarria. Ez da sekretu kosmiko bat, baina bai ordenaren inguruko zantzua. Eta agian horretan datza benetako xarma: sinpletasunetik edertasuna lortzeko duen gaitasunean.

Orri-oinak

¹ Zenbaki irrazional bat bi zenbaki osoren zatidura moduan idatz ezin daitekeen zenbaki erreala da, adibidez, π, e edo √2.

Erreferentziak